Intuitively speaking, how many times does half of a thing fit into a quarter of a thing? The answer is, exactly one half time.
this post was submitted on 14 May 2024
434 points (88.5% liked)
Memes
45536 readers
403 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 5 years ago
MODERATORS
How many halves fit into a quarter? Half of them
That's exactly how I think of it, so strange someone downvoted you
✅ Math is hard
❌ This math is hard
0.25 / 0.5 = 0.5
0.25 = 0.5 × 0.5
1/4 = 1/2 × 1/2
p/q=q
So q=√p
Works with a lot of numbers ☝🏻🤓
Ehhh |q| = √p but close enough
If q=√p then -q=√p also.
This is why "divide by half" and "divide in half" are two different things
It won’t keep you up if you just think of Divide as just multiplying by the fraction
Yeah I was gonna comment that 0.25*(1/0.5) = 0.5 doesn't look nearly as weird
I didn’t specify fully, but I was just thinking 1/4 * 2/1
Imo, as soon as you write it as 0.25 multiplied by a fraction it works, because you can then easily see that it's the same as (1/4)*2
The math looks perfectly fine. But when people phrase "half of a quarter" I think they have (1/2)*(1/4) in mind, instead of 0.25/0.5
But this isn't "half of a quarter" this is "the reciprocal of a half, of a quarter"
Half of a quarter is 0.25/2 or 0.25*1/2
I know, but to me this meme doesn't make sense to me unless I assume the person reading the math Expression is interpreting its real world application.
25 / 5 = 5 and nobodies head exploded. That's just evaluating a math Expression. .25 / .5 = .5 is the same. It's not a "my brain can't comprehend how to evaluate expressions" as the meme suggests.
However, if someone who doesnt do much algebra thought to themselves "I need half of a quarter", then I could understand why their brain might "hurt" as the meme suggests, for a similar reason why adding 20 degree Celsius water to 20 degree Celsius water doesn't make 40 degree Celsius wate
I'm probably reading into it too much, but the meme just doesn't feel like a "mind fuck that keeps me up at night". I'm looking for reasons to try and explain it, but it's just a math expression at the end of the day
I think you nailed the confusion in this meme.
To simplify: it's confusing that ½ = 0.5, but 1/2 ≠ 1/0.5
I think the meme is an exaggeration of the situation for comedic effect. It just looks silly at first glance, I don't believe the OP is kept up at night by this, and is rather making a remark about how it doesn't instantly feel intuitive as a result (to use the 20 Celsius water example, its the same kind of momentary "wtf?" as 40 Celsius water not being twice as hot as 20 Celsius water. After a moment you remember "oh derp yeah we're missing 273.15 kelvin in this picture lol")
If you give half a person a quarter of a thing, how much would you be giving a full person? That's right baby, half a thing. Don't sweat it.
I worry that people who can get onto the internet find fractions a challenge.
I don't think this was shared because people are finding it a "challenge" it just looks funny.
It takes all of a few seconds for your actual mathematical processing to kick in and you go "oh yeah duh" but its just a funky little string of numbers.
It lives in the same camp as how none of the >3 whole multiples of 17 feel like multiples of 17. 68? Preposterous.
load more comments
(4 replies)
x / sqrt(x) = sqrt(x)
Damn who would've thought?
Divide by 1/2 or multiply with 2/1. It's an equivalent transformation.
I just think of division as how many times the right expression fits inside the left expression. 0.5 fits into 0.25 only 0.5 aka 1/2 times, because only half of it fits.
Precisely this. The people not getting the OP are why Common Core was developed.
The numbers between zero and one are where all of the fun is!
1×2=2
Wow. Much brain. Maths wow.
25/5=5
2.5/0.5=5
o.O
I think, it is the real world logic that makes it hard to grasp. If you divide something with something small it becomes bigger. Mathematically it's easy and makes sense, but it it's somehow not intuitive. Especially for young me :)
That's the same as 2/2=1 3/3=1 268/268=1 ...
load more comments
(1 replies)
This just comes down to the fact that "dividing by a fraction is the same as multiplying by the inverse of the fraction" is an easy rule to follow but not particularly intuitive. In natural language, when most people hear "divide by half" they're actually picturing "divide by two" in their head.
It’s going to be okay:
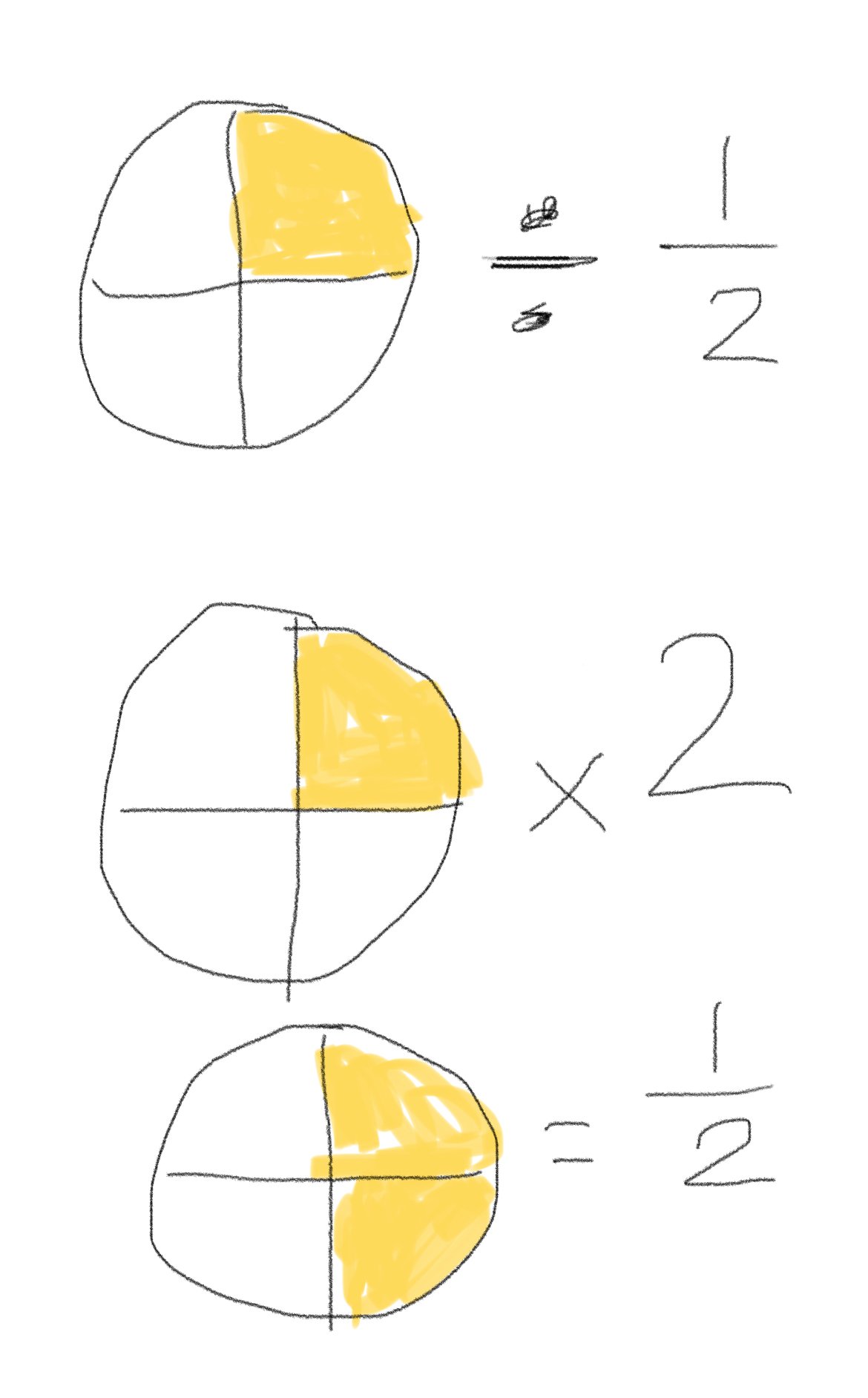
Edited to add this: Singapore math insists however, that we eliminate the use of visuals in describing arithmetic within the rationals. They encourage that users of common core rely upon the number line, and solely the number line for thorough and most mathematically sound representations of arithmetic, even when involving the division of fractions.
For those not up to speed to with common core, remember how the teacher used to draw a diagram of a bunny hopping from one integer to the next integer to represent adding given integers, such as 4+3, or -2+1? Imagine that representation being used with problems like 1/7 divided by 5/49, and no decimal approximation is allowed. It’s fascinating and truly something to appreciate from the standpoint of someone who truly loves mathematics. I think it makes for great discussions amongst math graduates like myself, and other math enthusiasts. What does that mean for those who are not so enthused? Sometimes it means the teacher receives death threats from angry students. You can’t make everyone happy.
I’m not sure I completely agree with the number-line-only approach, but I’m definitely sympathetic to it. It reinforces the idea that fractions are numbers like any other numbers, and not pieces of pizza.
I get that. I like the number line approach, and respect it, but I have also observed seasoned math coaches fumble the visual explanation of a division by fractions problem where the numerators and denominations were relatively prime. As soon as the guy had drawn the first fraction and began to say, “we’d multiply by the recipro-…”, I could tell it was going to be long problem. He just stood there, and then asked, “well, how would I go about explaining the ‘keep change flip’, if you will?” He ended the problem by saying he might just explain that the distance drawn for the first fraction needs to be repeated on the other side of the fraction to show the multiplication by the denominator of the second fraction, and then that distance could be broken into parts to demonstrate the division by the previous numerator of the second fraction.
Basically he ended the problem by saying, “let’s just reflect it! Then we can break it up.” There wasn’t really a sound justification for the reflection piece of the process, other than saying, “we need to multiply by the reciprocal of the second fraction, so we’ll just have to multiply by its denominator it had, prior to flipping it.”
That was the quietest meeting I have ever seen amongst that group of adults.
This don't avoid to sleep not even for 1/2 second. But pick any number. If that number is even, divide it by 2. If it's odd, multiply it by 3 and add 1. Now repeat the process with your new number. If you keep going, you'll eventually end up at 1.
You can't prove that!
Yes, but everyone tried since a century to find a number with which it don't work, good to avoid sleep.
Any positive number?
Multiplication of x times 6:
x * 6 = 1/2 x * 10 + x
This can sometimes be a shortcut for numbers that are easier to divide by 2 than to multiply by 6.
Take half as tens and add the number.
6 * 6 = 30 + 6 = 36
8 * 6 = 40 + 8 = 48
150 * 6 = 750 + 150 = 900
320 = 1600 + 320 = 1920
Etc.
Sleep well.
2^-2 * (2^-1)^-1 = 2^-2 * 2^(-1 * -1) = 2^(-2 + -1 * -1) = 2^(-2 + 1) = 2^-1 = 1/2 = 0.5
view more: next ›