proprietary, btw
Hint:
spoiler
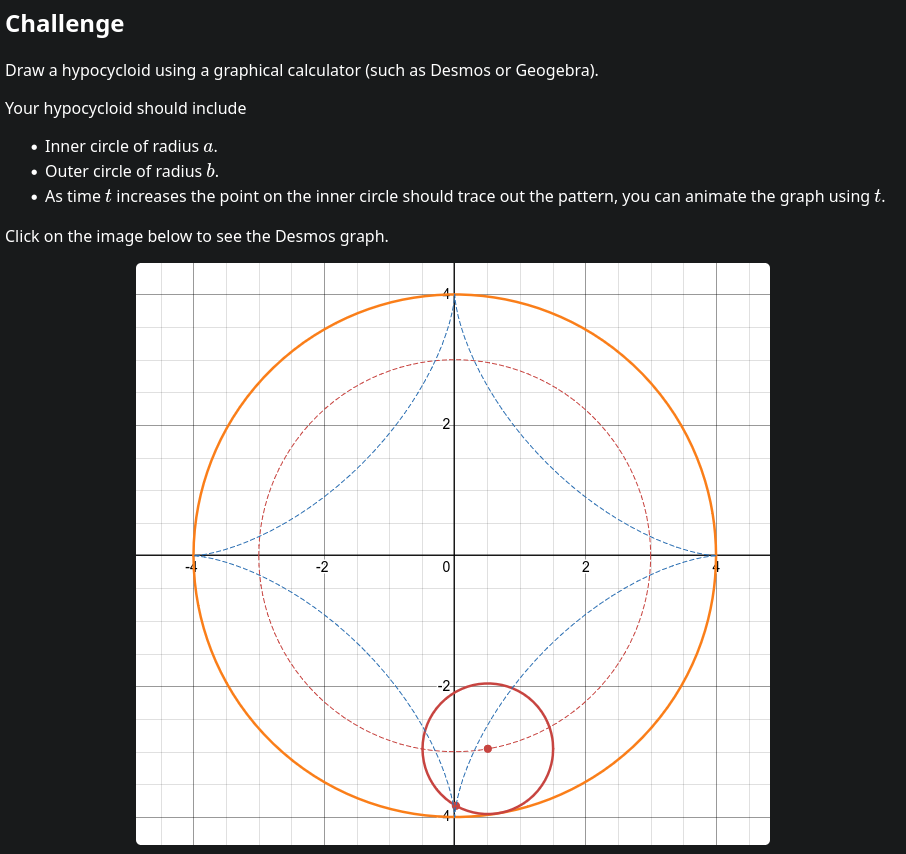
Try out the following tasks before going for the big one
- Draw a circle of radius
a. - Animate a point on circle
a, let that be your rotational speed. - Animate a circle rolling horizontally (along the
xaxis) at your rotational speed. - Animate a point on that horizontally rolling circle.
You should now have an idea on how to draw a hypocycloid.
Hint
spoiler
If you are studying the algorithm, you are doing it wrong
Solution: https://gmtex.siri.sh/fs/1/School/Extra/Maths/Qotd%20solutions/2024-08-04_extended-euclid.html
spoiler

Hint:
spoiler
Let x mod y = a
Solution: https://gmtex.siri.sh/fs/1/School/Extra/Maths/Qotd%20solutions/2024-08-01_multiple-of-modulus.html
spoiler

Hint:
spoiler
The size of a set is the number of possible values that an element can take.
because I have never heard of this argument before, ever. most media's stance on politics is "their party bad our party good", but the "all the parties are pretty hypocritical" argument has never been explored properly, because its depressing and nobody likes it.
yup thats the intended solution, im not really familiar with taylor series yet, but maybe for a person who knows taylor series would be able to see it right away
Hint
spoiler
The solution I have in mind is related to the Taylor series
Hint 2
spoiler
It converges to -ln(2), but why
Solution:
i main zathura, but okular is a good one as well
Here's a rly cool solution from stackexchange, which blows my average geometric solution out of the water
spoiler

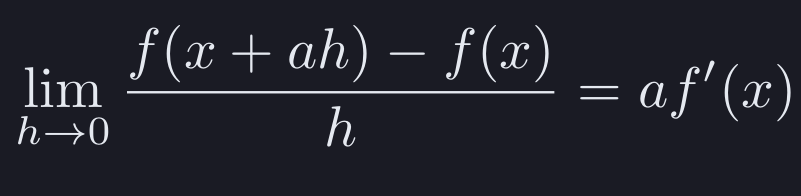










That would maybe make sense.
Yeah I think the claim might be true, but still there are probably ways to not hit a UN base of fixed location while carrying out an offensive.
This detail wasn't here this morning, the article is gradually edited as more info surfaced. See the url for the original title.