It amazes me that people write financial software in JS. What can possibly go wrong :D
this post was submitted on 07 Sep 2022
56 points (93.8% liked)
Programmer Humor
32070 readers
673 users here now
Post funny things about programming here! (Or just rant about your favourite programming language.)
Rules:
- Posts must be relevant to programming, programmers, or computer science.
- No NSFW content.
- Jokes must be in good taste. No hate speech, bigotry, etc.
founded 5 years ago
MODERATORS
How? What? Is this real? Could someone explain why? Is there a use?
The source of this appears to be that 0.0000001.toString() == "1e-7". Presumably parseInt first converts its argument to a String (which kinda makes sense).
Of course the more important question is why are you passing a number to parseInt?
And it works properly if you change it from a float to a strong first! JavaScript 🥰
2**53 + 1 == 2**53
That's just floating-point arithmetics for you
(The parseInt thing however... I have absolutely no idea what's up with that.)
How?
IIRC it's called absorption. To understand, here's a simplified explanation the way floating-point numbers are stored (according to IEEE 754):
- Suppose you're storing a single-precision floating point number — which means that you're using 32 bit to store it.
- It uses the following format: The first bit is used for the sign, the next 8 bit are the exponent and the rest of the bits is used for the mantissa. Here's a picture from Wikipedia to illustrate:
- The number that such a format represents is
2 ^ (exponent - 127) * 1.mantissa. The 127 is called a bias and it's used to make possible to represent negative exponents.1.mantissameaning that for example, if your mantissa is1000000..., which would be binary for0.5, you're multiplying with1.5. Most (except for very small ones) numbers are stored in a normalized way, which means that1 <= 1.mantissa < 2, that's why we calculate like this and don't store the leading1.in the mantissa bits.
Now, back to 2**53 (as a decimal, that's 9007199254740992.0). It will be stored as:
0 10110100 00000000000000000000000
Suppose you're trying to store the next-bigger number that's possible to store. You do:
0 10110100 00000000000000000000001
But instead of 9007199254740993.0, this is representing the number 9007200328482816.0. There is not enough precision in the mantissa to represent an increment by one.
I don't remember how exactly this works, but any number that you're storing as float gets rounded to the nearest representable value. 2**53 + 1 will be represented by the same bit-string as 2**53, since it's impossible to represent 2**53 + 1 exactly with the given precision (it's not possible with double-precision either, the next representable number in double-precision would've been 2**53 + 2). So when the comparison happens, the two numbers are no longer distinguishable.
Here's a good website to play around with this sort of thing without doing the calculations by hand: https://float.exposed Wikipedia has some general information about how IEEE 754 floats work, too, if you want to read more.
Disclaimer that this is based on my knowledge of C programming, I never programmed anything meaningful in JavaScript, so I don't know whether the way JavaScript does it is exactly the same or whether it differs.
...but why? This looks like it would never be expected behavior. Like a bug in the implementation, which can simply be fixed.
Oh no, it's even documented on MDN:
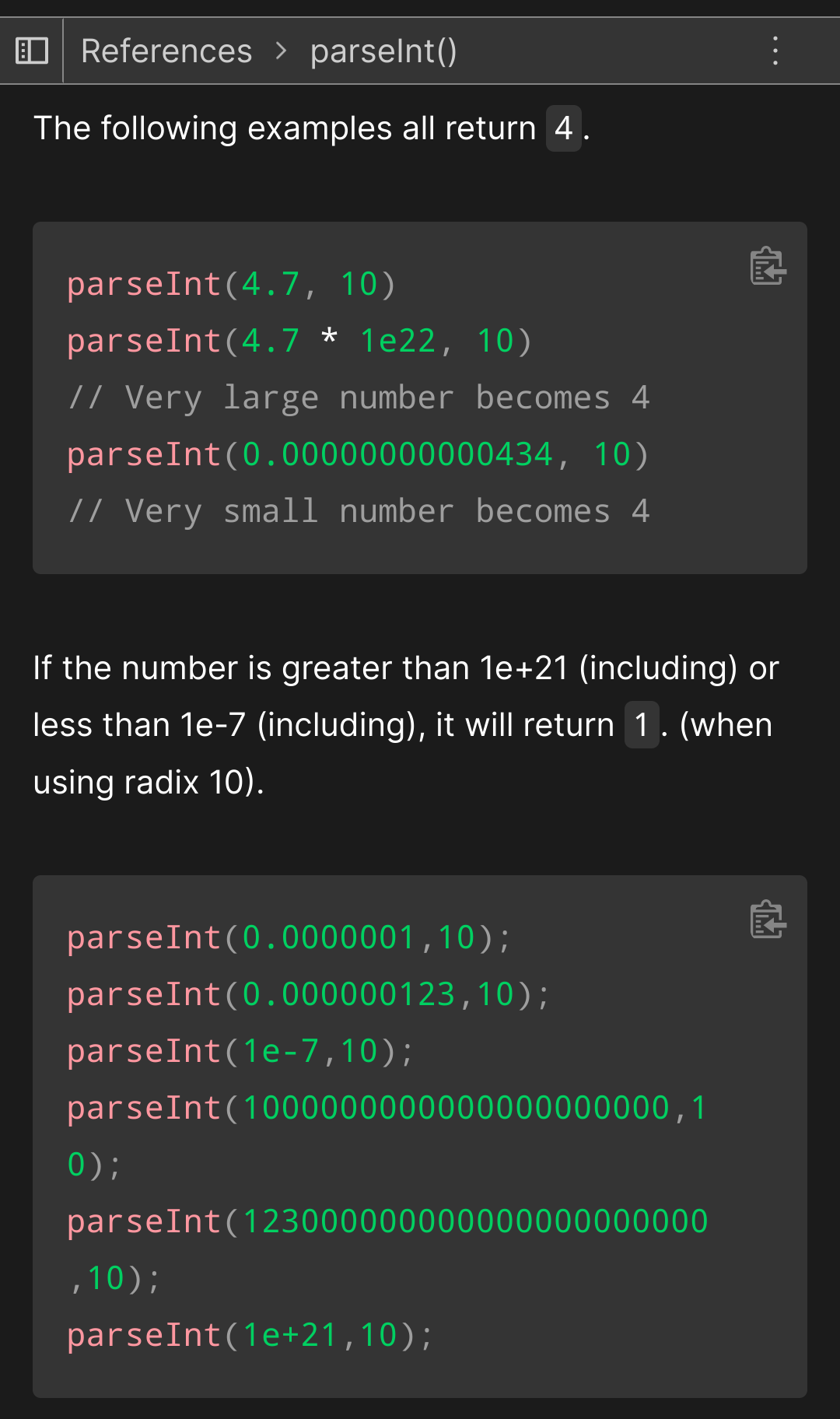
Every time I have to write code in jabbascript I think "can't be that hard" but then I stumble across some weird behavior like this and I first think "must be a bug somewhere in my code" but no. After some research it always turns out it's actually a documented "feature(?)".
I have no idea why this shitty language is so popular and the web standard.
jabbascript
Should becomes standard
Sweet Flying Spaghetti Monster, that's horrible. I'm guessing the reason is to keep the truth value equivalent when casting to boolean, but there has to be a more elegant way....
Javascript in a nutshell
Technically, the top and bottom lines on classical math approach 1 and 0, like limits.
As far as I'm aware, there's actually no consensus on what's technically correct.
Some will argue that they don't approach these values, because you're not saying lim x from 0 to ∞, where x is the number of '9'-digits. Instead, you're saying that the number of digits is already infinite right now.